차원의 저주란
차원: 데이터에서설명 변수(컬럼)를 의미, 변수가 많을수록 더 많은 정보 담음- 차원이 많은 데이터는 더 많은 정보를 포함하고 있어, 분석에 있어 결과 정확성 높여줄 수 있음
차원의 저주:데이터의 차원이 높아질수록 분석 성능이 떨어지는 경우가 발생- 변수가 많을수록 모델이 과적합되거나 학습이 어려워질 수 있기 때문
- 높아지는 차원에 비해 데이터의 밀도와 비중이 떨어지기에, 모델이 활용할 수 있는 데이터의 양이 상대적으로 모자라기 때문(데이터의 비중이 떨어지는 차원의 예측에 대해서는 심하게는 단 하나의 데이터를 그대로 암기해버릴 수도 있는 것)
차원의 축소
- 차원의 저주를 해결하기 위해
차원 축소(Dimensionality Reduction)사용 - 차원 축소는 데이터의
변수(차원) 수를 줄여성능을 개선하는 방법
1. 차원 선택 (Feature Selection)
- 전체 변수 중 의미 있는 것만 선택해 분석에 사용하는 방법.
- 각 변수 간의 중복성을 고려해 불필요하거나 덜 중요한 변수를 제거하는 방식입니다.
차원 선택의 장단점
[ 장점 ]
- 쉽고 직관적, 제거할 변수를 간단히 판단하고 선택하면 되기 때문에 빠르게 적용 가능
- 변수의 특성이 유지되어 결과를 쉽게 해석 가능
[ 단점 ]
- 정보 손실 큼, 제거한 변수는 일부 정보를 제공했을 수 있으나, 해당 정보는 손실
2. 차원 추출 (Feature Extraction)
- 새로운 차원을 생성해 여러 변수의 특징을 하나의 변수로 요약하는 방식
- 여러 변수의 공통 특성을 종합해
새로운 변수(주성분)를 생성하여 차원 축소 - 가장 대표적인 방법 :
PCA(Principal Component Analysis)- PCA는 변수 간의 분산을 분석해 가장 중요한 축(주성분)을 찾고, 이를 통해 데이터의 차원을 축소
차원 추출의 장단점
[ 장점 ]
- 정보 손실이 적음: 중요한 정보를 최대한 유지하면서 차원을 줄임
- 고차원 데이터를 효율적으로 처리
[ 단점 ]
- 새로 생성된 변수는 해석이 어려움: 주성분이 어떤 의미를 가지는지 이해하기 어려울 수 있음
- 계산 비용 증가: 추가 연산이 필요함
PCA (Principal Component Analysis)
[ 정의 ]
- 여러 차원의 데이터를 가장 잘 설명하는
주성분(Principal Component)을 찾아 차원을 축소하는 기법 데이터를 축소하는 과정에서정보 손실을 최소화하면서도, 주요 특성을 유지할 수 있도록 설계
[ PCA 과정 ]
1. 데이터 표준화 및 원점 이동
- PCA를 적용하기 전에
변수 간 단위를 통일해야 함 - 각 변수의 값이 다를 경우, 단위가 큰 값이 결과에 더 많은 영향을 미칠 수 있기 때문
- 이를 위해
표준화(Standardization)적용표준화를 통해 좌표계에서 원점을 중심으로 재정렬
2. 주성분 찾기 ( .fit() )
- PCA에서는
주성분을 찾아데이터의 분산을 가장 잘 설명하는 선을 구함
첫 번째 주성분(PC1): 데이터 분산을가장 잘 설명하는 축두 번째 주성분(PC2): 첫 번째 주성분에수직인 축으로,남은 분산을 설명하는 선- 가장 잘 설명하는 것의 수직, 즉 반대이므로 가장 잘 분산을 설명하지 못하는 축
3. 데이터 투영 ( .transform() )
- 주성분을 찾으면
데이터를 그 주성분에 투영 - 주성분 위에 데이터를
옮기는 과정을 의미하며, 이를 통해새로운 축(PC1, PC2)에 데이터를 나타냄- 기존 데이터의 정보를 반영, 보존 -> 차원 선택과 달리 손실 최소화
- 수직 거리가 줄어들면
선의 길이( 투영점-원점(평균) )가 커져 데이터 분산이 최대화
4. 축 회전 ( .transform() )
- 새롭게 정의된
PC1과 PC2를 x축, y축으로 설정해 데이터를회전시킴 - 이로 인해 기존의 변수가 사라지고,
PC1과 PC2라는 새로운 축으로 데이터를 나타낼 수 있게 됨
5. 차원 축소
찾은 주성분을 사용해 차원을 축소
- ex)
PC1만사용해 데이터를 표현 > 1차원 - ex)
PC1과 PC2를 사용해 데이터를 표현 > 2차원
from sklearn.decomposition import PCA
from sklearn.preprocessing import StandardScaler
import matplotlib.pyplot as plt
import pandas as pd
import seaborn as sns
user_df = pd.read_csv("../data/custom_data.csv")
# 데이터 표준화
scaler = StandardScaler()
scaled_data = scaler.fit_transform(user_df)
# PCA 적용
pca = PCA(n_components=2)
pca_data = pca.fit_transform(scaled_data)
# PCA 설명력
explained_variance = pca.explained_variance_ratio_
# PCA 결과 시각화
plt.figure(figsize=(8, 6))
sns.kdeplot(x=pca_data[:, 0], y=pca_data[:, 1], fill=True, cmap="Blues", alpha=0.6)
sns.scatterplot(x=pca_data[:, 0], y=pca_data[:, 1])
plt.xlabel(f"PC1 ({explained_variance[0]*100:.2f}%)")
plt.ylabel(f"PC2 ({explained_variance[1]*100:.2f}%)")
plt.title("PCA with Explained Variance")
plt.show()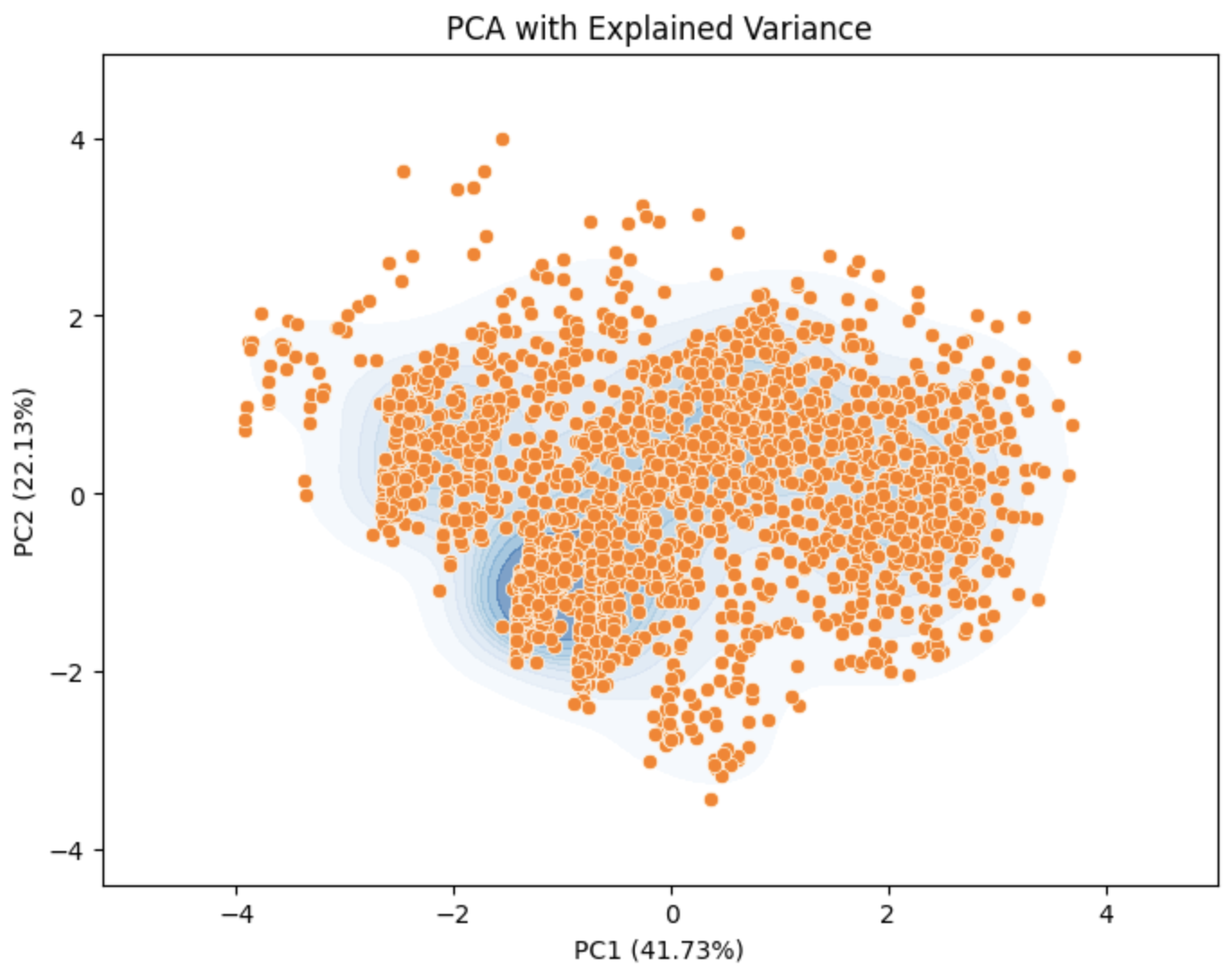
PCA 과정 파이썬 코드
- PCA 모델 생성
import pandas as pd from sklearn.preprocessing import StandardScaler from sklearn.decomposition import PCA
user = pd.read_csv('../data/custom_data.csv')
표준화
scaler= StandardScaler()
scaled_df = scaler.fit_transform(user)
PCA (n_components : 주성분 개수)
pca = PCA(n_components=2)
2. PCA 학습 및 변환
```python
# pca.fit() #주성분 찾기
# pca.transform() #투영 및 축 회전, 새로운 변수 생성
scaled_df_pca = pca.fit_transform(scaled_df)
pca_df = pd.DataFrame(scaled_df_pca, columns = ['PCA1', 'PCA2'])
pca_df.head()- 결과 확인 및 해석
# 시각화 import seaborn as sns import matplotlib.pyplot as plt
sns.scatterplot(data=pca_df, x='PCA1', y='PCA2')
plt.show()
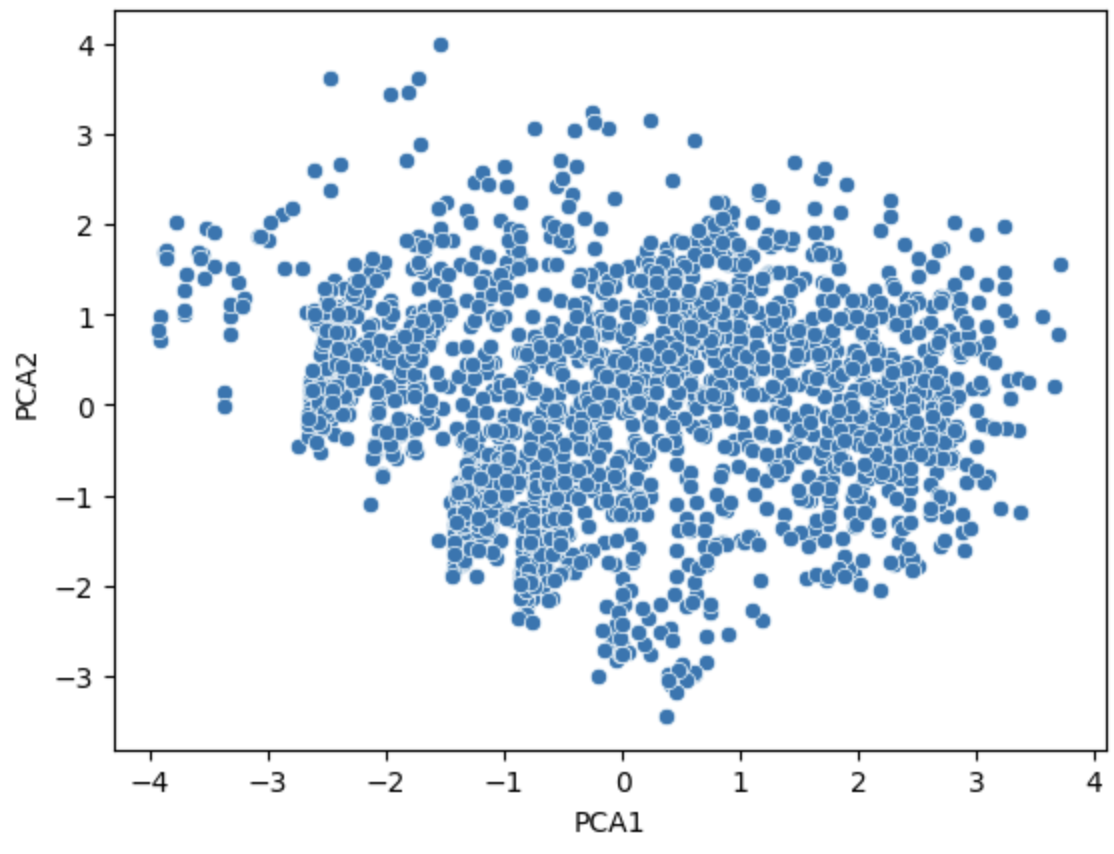
### [ 적절한 주 성분 개수 찾기 ]
#### 1. Scree Plot 생성
- `Scree Plot`을 통해 `각 주성분이 전체 데이터에 대해 설명하는 분산 비율`을 확인
- `explained_variance_ratio_` 속성을 사용하여 각 주성분의 분산 설명력 비율을 계산
```python
pca.explained_variance_ratio_# 총합은 1
pca.explained_variance_ratio_.sum()import numpy as np
import matplotlib.pyplot as plt
# 주성분의 분산 비율
num_components = len(pca.explained_variance_ratio_)
# x = np.arange(num_components)
# x = ['PC1', 'PC2', 'PC3', 'PC4', 'PC5', 'PC6']
x = pca_df.columns
var = pca.explained_variance_ratio_
# Bar Plot (Scree Plot)
plt.bar(x, var)
plt.xlabel('PC')
plt.ylabel('Variance Ratio')
plt.title('Scree Plot')
plt.show()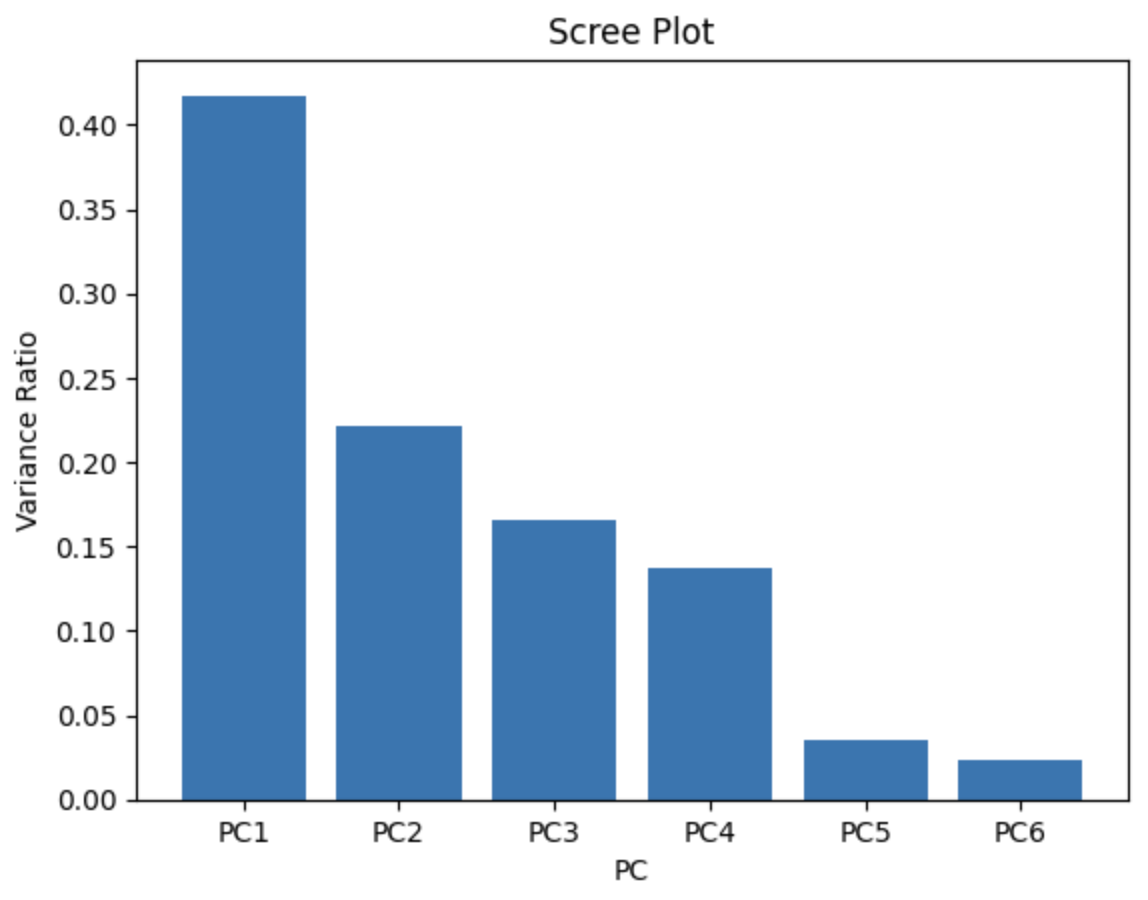
2. 누적 분산 비율 계산
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
# 누적 분산 비율 계산
cum_var = np.cumsum(var)
# 누적 분산 비율 데이터프레임 생성
cum_var_df = pd.DataFrame({'cum_vars': cum_var}, index=pca_df.columns)
cum_var_df# 누적 분산 비율 꺾은선 그래프
plt.figure(figsize=(8, 6))
plt.plot(cum_var_df.index, cum_var_df['cum_vars'], marker='o', label='Cumulative Variance')
plt.axhline(y=0.7, color='r', linestyle='--', label='70% Threshold')
# 누적합이 70%에 도달하는 지점에 수직 파선 추가
threshold_index = np.argmax(cum_var >= 0.7) # 최대값의 왼쪽부터 첫 인덱스
plt.axvline(x=cum_var_df.index[threshold_index], color='g', linestyle='--', label=f"PC{threshold_index+1}")
# 그래프 제목과 축 레이블 추가
plt.title("Cumulative Variance Explained by Principal Components")
plt.show()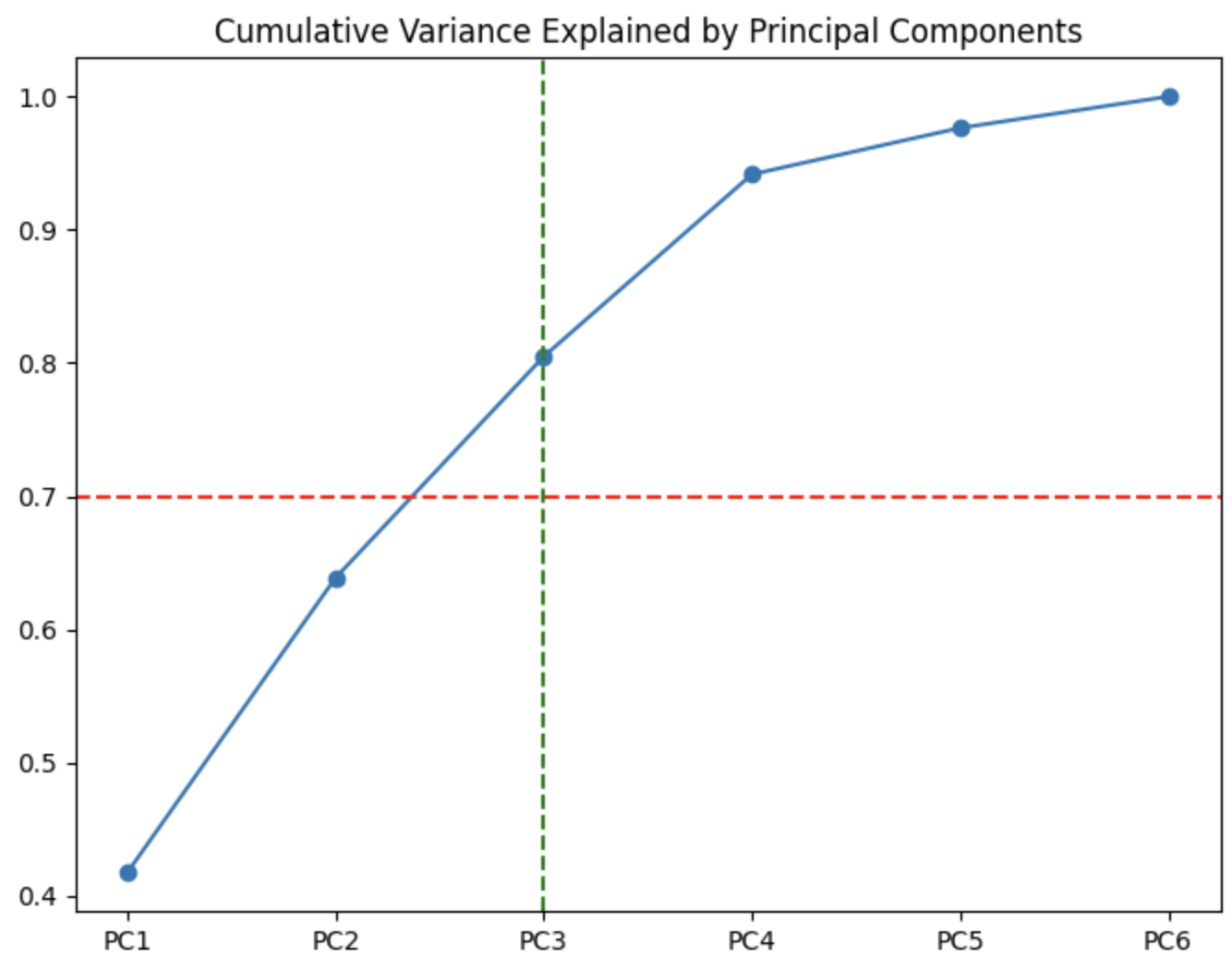
결과 해석
- Scree Plot과 누적 분산 비율을 통해 주성분을 선택 가능
- ex)
PC1과 PC2가 데이터의 약 60%를 설명,PC3까지 포함하면 약 80% 설명력을 갖게 됨 - PCA 주성분 선택의 기준은
누적 설명력이 70% 이상이 되는 주성분을 선택하는 것
[ 장단점 ]
장점
- 정보 손실 최소화
- PCA는 데이터의 주성분 을 찾아내기 때문에, 차원 축소 과정에서 변수 간의 중요한 정보 최대한 보존 가능
- 변수 종합 반영
- 각 주성분은 기존 변수들의 특징을 종합적으로 반영하여 축소된 차원으로 변환
- 모델 성능 개선
- 차원 축소를 통해 불필요한 노이즈를 제거하고, 보다 정확하고 일반화된 예측 모델 학습 가능
단점
- 해석의 어려움
- PCA는 여러 변수의 특징을 종합하여 주성분을 도출하기 때문에, 주성분의 의미를 명확하게 해석하기가 어려움
- 주성분은 하나의 변수에 매칭되지 않고, 여러 변수의 영향 받음
- 계산 비용
- 차원이 증가할수록 계산 비용이 증가하고 연산 시간이 오래 걸릴 수 있음
'DA Study > Data Analytics' 카테고리의 다른 글
| [통계] 모집단, 표준편차, 분산, 평균, 확률, 확률분포, 이산확률변수, 연속확률변수, 확률밀도함수 (0) | 2024.12.30 |
|---|---|
| [통계] 피어슨 상관계수와 공분산 (1) | 2024.12.28 |
| [데이터 시각화] Matplotlib으로 데이터 시각화하기 (2) | 2024.12.17 |
| [데이터 분석] 클러스터링 모델들 - 덴드로그램(Dendrogram) / DBSCAN / GMM (0) | 2024.12.17 |
| [데이터 분석] 클러스터 분석, K-MEANS (0) | 2024.12.16 |